 Faltwerkselement
Faltwerkselement
Über diesen Dialog definieren Sie Faltwerkselemente. Dies sind flächige Tragglieder, wie z.B. Deckenplatten, Wandscheiben oder Dachflächen. Die Umrandung eines Faltwerkselementes ist ein Polygon aus dreidimensionalen Knoten.
Die Form des Polygons ist beliebig. Die Polygonpunkte müssen aber alle in einer Ebene liegen und die Kanten des Polygonzuges dürfen sich nicht schneiden.
Innerhalb eines Faltwerkelementes können Aussparungen angeordnet werden.
Die Form des Polygons ist beliebig. Die Polygonpunkte müssen aber alle in einer Ebene liegen und die Kanten des Polygonzuges dürfen sich nicht schneiden.
Innerhalb eines Faltwerkelementes können Aussparungen angeordnet werden.
Eigenschaften Ausrichtung Hilfslinien Elastische Bettung Variable Dicke Orthotropie Sonstiges
Name
Ein eindeutiger Bezeichner für dieses Objekt. Dabei handelt es sich um den Namen, unter dem das Objekt identifiziert wird. Objekte von unterschiedlichem Typ dürfen identische Namen haben.
Dicke
Das Faltwerkselement kann entweder eine konstante oder eine linear veränderliche Dicke besitzen. Für den Regelfall einer konstanten Dicke wird diese hier eingegeben.
 Material
Material
Material des Faltwerkelementes. Jedem Faltwerkselement muss ein Material zugewiesen werden. Dieses wird für die Schnittgrößenberechnung und die Bemessung benötigt.
Siehe auch: Material
 Neu...
Neu...
Klicken Sie auf diesen Button, wenn Sie ein neues Material anlegen möchten. Daraufhin erscheint der Dialog zum Anlegen eines neuen Materials. Wählen Sie das gewünschte Material aus und beenden den Dialog mit "OK". Der Name des neuen Materials wird im Feld angegeben.
 Bemessungsparameter
Bemessungsparameter
Neben den Schnittgrößen wird im Regelfall auch eine Bemessung des Systems durchgeführt.
Zur Durchführung der Bemessung müssen wesentlich mehr Eingangswerte als für die Schnittgrößenberechnung festgelegt werden. Man unterscheidet folgende Parametertypen:
Zur Durchführung der Bemessung müssen wesentlich mehr Eingangswerte als für die Schnittgrößenberechnung festgelegt werden. Man unterscheidet folgende Parametertypen:
- Materialabhängige: Diese werden bei der Wahl der Materials festgelegt.
- Querschnittsabhängige: Diese werden bei der Wahl des Querschnitts festgelegt.
- Normabhängige: In dieser Kategorie sind all diejenigen zusammengefasst, die nicht zu den ersten beiden gehören. Dazu gehört z.B. bei der Betonschubbemessung die Neigung der Schubbewehrung oder bei der Holzbemessung die Erhöhungen der zulässigen Spannungen.
Siehe auch: Bemessungsparameter
 Neu...
Neu...
Klicken Sie auf diesen Button, wenn Sie einen neuen Bemessungsparameter anlegen möchten. Daraufhin erscheint der Dialog zum Anlegen eines neuen Bemessungsparameters. Geben Sie dort die Kennwerte für diesen Parameter ein und beenden den Dialog mit "OK". Der Name des neuen Bemessungsparameter wird angezeigt.
 Bewehrungsanordnung
Bewehrungsanordnung
Bei Faltwerkselementen aus Beton muss die Lage der Bewehrung festgelegt werden.
Siehe auch: Bewehrungsanordnung
 Neu...
Neu...
Klicken Sie auf diesen Button, wenn Sie eine neue Bewehrungsanordnung anlegen möchten. Daraufhin erscheint der Dialog zum Anlegen einer neuen Bewehrungsanordnung. Geben Sie dort die Kennwerte für diese Anordnung ein und beenden den Dialog mit "OK". Der Name der neuen Bewehrungsanordnung wird angezeigt.
Zuschlag
Der Zuschlag für Putz und Belag, angegeben in kN/m². Wird bei Lastfällen mit berücksichtigtem Eigengewicht als Flächeneinwirkung in die Berechnung einbezogen. Auch dann, wenn beim Faltwerk die Option 'Eigengewicht berücksichtigen' ausgeschaltet ist.
Drillsteifigkeit
Die Drillsteifigkeit einer Platte ist z.B. der Grund dafür, dass sich die Ecken von vierseitig gelagerten Platten hochwölben. Je geringer die Drillsteifigkeit ist, umso weniger wölben sich die Plattenecken nach oben und umso grösser werden die Feldmomente. Dies führt auch dazu, dass die abhebenden Auflagerkräfte in den Ecken verschwinden.
Die Eingabe von 100 berechnet eine Platte mit voller Drillsteifigkeit. Je geringer der eingegeben Wert ist, um so kleiner wird auch die Drillsteifigkeit. Die Eingabe von 0 ist nicht möglich, da dadurch die Platte instabil werden würde.
Die Eingabe von 100 berechnet eine Platte mit voller Drillsteifigkeit. Je geringer der eingegeben Wert ist, um so kleiner wird auch die Drillsteifigkeit. Die Eingabe von 0 ist nicht möglich, da dadurch die Platte instabil werden würde.
Am folgenden Beispiel einer vierseitig gelagerten Platte soll die Auswirkung der Drillsteifigkeit erläutert werden.
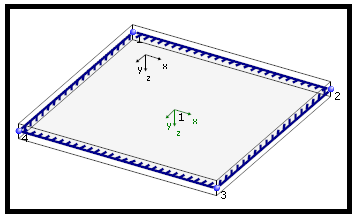
| Drillsteifigkeit 100.00 % | Drillsteifigkeit (fast) 0.00 % | ||
| mx |  |  | Bei kleiner Drillsteifigkeit werden die Feldmomente größer. |
| mxy |  |  | Bei kleiner Drillsteifigkeit werden die Drillmomenten kleiner. |
| Auflagerkräfte |  |  | Bei kleiner Drillsteifigkeit werden sowohl die Eckkräfte als auch die Kräfte in Lagermitte kleiner. |
Kriechzahl phi nach 3.1.4.
Bei Bauteilen aus Beton kann eine Berechnung im Zustand 2 durchgeführt werden. Die für diese Berechnung notwendige Kriechzahl phi nach 3.1.4. wird an dieser Stelle definiert.
Die Schwinddehnung eps,cs wird bei den Bemessungsparametern festgelegt.
Siehe auch: Bemessungsparameter
Eckpunkte
Die Eckpunkte (Knotennamen) des Polygonzuges des Faltwerkselements. In diesem Eingabefeld können Sie die beteiligten Eckpunkte editieren. Sie können neue Knoten aufnehmen und vorhandene löschen. Die Namen der Knoten müssen dabei durch ein ";" getrennt werden.
Eigengewicht berücksichtigen
Bei jedem Lastfall können Sie angeben, ob in diesem das Eigengewicht des Systems berücksichtigt werden soll. Wenn dieser Schalter aktiviert ist, wird das Eigengewicht dieses Elementes berücksichtigt. Ist der Schalter deaktiviert, wird das Eigengewicht nicht berücksichtigt.
Darstellung
Alle Elemente, die in der Graphik dargestellt werden, werden von Haus aus mit vorgegebenen Eigenschaften wie Farben, Schriftarten und Strichstärken angezeigt. Die vorgegebenen Darstellungsarten für alle Objekte können Sie unter "Optionen → Einstellungen" verändern. Darüber hinaus kann jedes einzelne Objekt - also jeder einzelne Knoten, Balken, ... - eine eigene Darstellungsart mit anderen Parametern für Farben, Strichstärken, usw. haben. Dadurch ist es beispielsweise möglich, Elemente stockwerksweise mit unterschiedlichen Farben zu versehen.
Wählen Sie hier die Darstellungseigenschaften für dieses Objekt aus. Wenn "Nichts ausgewählt" ist, werden die unter "Optionen → Einstellungen" vorgegebenen Parameter verwendet.
Wählen Sie hier die Darstellungseigenschaften für dieses Objekt aus. Wenn "Nichts ausgewählt" ist, werden die unter "Optionen → Einstellungen" vorgegebenen Parameter verwendet.
 Neu...
Neu...
Klicken Sie auf diesen Button, um einen neuen Satz an Darstellungsparametern anzulegen und dem Objekt zuzuweisen.
Kommentar
Der Kommentar zu diesem Faltwerkselement.
Jedes Faltwerkselement kann in den folgenden Richtungen elastisch gebettet werden:
| Längsbettung | in lokaler X-Richtung | Reibung |
| Querbettung | in lokaler Y-Richtung | Reibung |
| Querbettung | in lokaler Z-Richtung | Senkrechter Druck |
Bettung in lokal X,Y,Z
Geben Sie hier den Bettungsmodul für die jeweilige Richtung an.
Ausschluss der Bettung
Die Gründung eines Bauwerkes kann im Regelfall nur Druck aufnehmen. An Stellen, an denen das Fundament abhebt, wird es in seiner Bewegung durch die Gründung nicht behindert. Die Bettung wirkt somit nur in einer Richtung(Entgegen der Gründung). In diesem Fall müssten Sie die Bettung ausschließen.
Folgende Ausschlussmöglichkeiten können gewählt werden:
Folgende Ausschlussmöglichkeiten können gewählt werden:
- ohne Ausschluss
- Ausschluss bei Bewegung in positiver Richtung der Achse des lokalen Koordinatensystems
- Ausschluss bei Bewegung in negativer Richtung der Achse des lokalen Koordinatensystems
 Kompletter Bettungsausfall bei Ausfall einer Bettungskomponente
Kompletter Bettungsausfall bei Ausfall einer Bettungskomponente
Für ein Faltwerkselement kann die Bettung in 3, voneinander unabhängigen, Richtungen angegeben werden. Auf diese Art kann die Bettung z.B. in lokaler Z-Richtung ausfallen, in den anderen Richtungen aber noch wirksam sein. Wenn Sie diesen Schalter betätigen, fallen die Bettungen in den anderen Richtungen automatisch mit aus, sobald nur eine einzige ausfällt.
 Dicke ist konstant
Dicke ist konstant
Im Regelfall besitzen Faltwerkselemente eine konstante Dicke. Es lassen sich aber auch beliebige angevoutete Elemente berechnen. In diesem Fall müssen Sie die Höhe an drei Stellen des Elementes definieren. Die Höhen an allen anderen Stellen ergeben sich so automatisch.
 Knoten 1
Knoten 1
Der Knotenname für die erste Position der Dickenangabe.
Siehe auch: Knoten
Dicke 1
Die Dicke des Faltwerkselements bei der ersten Position. [cm]
 Knoten 2
Knoten 2
Der Knotenname für die zweite Position der Dickenangabe.
Siehe auch: Knoten
Dicke 2
Die Dicke des Faltwerkselements bei der zweiten Position. [cm]
 Knoten 3
Knoten 3
Der Knotenname für die dritte Position der Dickenangabe.
Siehe auch: Knoten
Dicke 3
Die Dicke des Faltwerkselements bei der dritten Position. [cm]
 Auswählen (Knoten 1, 2 bzw. 3)
Auswählen (Knoten 1, 2 bzw. 3)
Klicken Sie auf diesen Button, um den entsprechenden Knoten mit der Maus festzulegen. Nachdem Sie auf den Button geklickt haben, verschwindet der Eigenschaftsdialog, und Sie haben freie Sicht auf das Arbeitsfenster. Bewegen Sie dann die Maus in der Graphik. Wenn sich der Mauscursor in der Nähe eines Knotens befindet, wird der Knoten mit einem gelben Rechteck und dem Knotennamen markiert.
Um diesen Knoten auszuwählen, klicken Sie einmal mit der linken Maustaste in das innere Quadrat des gelben Rechtecks. Daraufhin erscheint der Eigenschaftsdialog wieder und der Name des Knotens wird in das Textfelder für den Knoten eingetragen. Wenn Sie die Auswahl abbrechen möchten, ohne einen Punkt auszuwählen, klicken Sie stattdessen einmal mit der rechten Maustaste.
Um diesen Knoten auszuwählen, klicken Sie einmal mit der linken Maustaste in das innere Quadrat des gelben Rechtecks. Daraufhin erscheint der Eigenschaftsdialog wieder und der Name des Knotens wird in das Textfelder für den Knoten eingetragen. Wenn Sie die Auswahl abbrechen möchten, ohne einen Punkt auszuwählen, klicken Sie stattdessen einmal mit der rechten Maustaste.
Jedes Faltwerkselement besitzt ein lokales Koordinatensystem, in dessen XY-Ebene sich alle seine Eckpunkte befinden. Man hat die Möglichkeit, das lokale Koordinatensystem manuell festzulegen oder automatisch erzeugen zu lassen. Nicht nur die Eckpunkte sind in diesem Koordinatensystem definiert. In diesem Koordinatensystem werden neben den Eckpunktkoordinaten auch weitere Eigenschaften definiert:
Bei automatischer Ausrichtung des Koordinatensystems ergibt sich die Ebene des Faltwerkselements durch die Lage seiner Eckpunkte. Die X-Achse wird innerhalb dieser Ebene derart gewählt, dass diese parallel zur globalen XY-Ebene liegt und einen möglichst kleinen Winkel mit der globalen X-Achse bildet. Als Y-Achse zeigt in Richtung der positiven Z-Achse des globalen Koordinatensystems.
Der Drehsinn der Eckpunkte oder die Nummerierung hat keinen Einfluss auf das Koordinatensystem.
Wenn man ein Faltwerkselement mit Hilfe einer Arbeitsebene erzeugt, werden alle die Ausrichtung betreffenden Einstellungen von dieser übernommen. Dabei werden die Einstellungen allerdings kopiert: Werden also nachträglich die Einstellungen der ursprünglich verwendeten Arbeitsebene verändert, so hat das keine Auswirkungen auf das Faltwerkselement.
Erstellt man ein Faltwerkselement ohne Verwendung einer Arbeitsebene, wird das lokale Koordinatensystem standardmäßig automatische erzeugt.
- Elastische Bettung
- Lokale Lasten auf dem Element
- Ergebnisse der Schnittgrößen in diesem Element
- Richtung der Bewehrung
Bei automatischer Ausrichtung des Koordinatensystems ergibt sich die Ebene des Faltwerkselements durch die Lage seiner Eckpunkte. Die X-Achse wird innerhalb dieser Ebene derart gewählt, dass diese parallel zur globalen XY-Ebene liegt und einen möglichst kleinen Winkel mit der globalen X-Achse bildet. Als Y-Achse zeigt in Richtung der positiven Z-Achse des globalen Koordinatensystems.
Der Drehsinn der Eckpunkte oder die Nummerierung hat keinen Einfluss auf das Koordinatensystem.
Wenn man ein Faltwerkselement mit Hilfe einer Arbeitsebene erzeugt, werden alle die Ausrichtung betreffenden Einstellungen von dieser übernommen. Dabei werden die Einstellungen allerdings kopiert: Werden also nachträglich die Einstellungen der ursprünglich verwendeten Arbeitsebene verändert, so hat das keine Auswirkungen auf das Faltwerkselement.
Erstellt man ein Faltwerkselement ohne Verwendung einer Arbeitsebene, wird das lokale Koordinatensystem standardmäßig automatische erzeugt.
Ursprung
Die Position, welche den Ursprung des lokalen Koordinatensystems festlegt.
X-Achse
Der Vektor, welcher die lokale X-Achse des lokalen Koordinatensystems festlegt. Muss nicht angegeben werden wenn das Koordinatensystem automatisch gewählt wird.
Vektor
Der Vektor, welcher zusammen mit der X-Achse die Ebene aufspannt. Die Y-Achse ergibt sich senkrecht zur X-Achse in dieser Ebene. Muss nicht angegeben werden wenn das Koordinatensystem automatisch gewählt wird.
 Automatisches Koordinatensystem
Automatisches Koordinatensystem
Ist diese Option eingeschaltet, so wird das lokale Koordinatensystem automatisch erzeugt. Hier ist die Ausrichtung des lokales Koordinatensystems erklärt.
Max. Kantenlänge der Netzmaschen
Hier wird die obere Grenze für die Kantenlänge der Maschen des FE-Netzes in diesem Faltwerkselement festgelegt. Je kleiner die Maschen sind, desto genauer aber auch zeitintensiver wird die Berechnung. [cm]
Biegetheorie
Über diesen Schalter legen Sie fest, welche Biegetheorie bei diesem Faltwerkselement verwendet werden soll.
Die Biegetheorie nach Mindlin berücksichtigt den Querkrafteinfluss realitätsnaher als die Biegetheorie nach Kirchhoff.
Die Biegetheorie nach Mindlin berücksichtigt den Querkrafteinfluss realitätsnaher als die Biegetheorie nach Kirchhoff.
Spezifischer Stahlverbrauch
Dieser Wert wird für die Ausgabe der Stahlmenge in der Stückliste verwendet. [kg/m³]
Orthotropie
Isotrope Flächen besitzen in allen Richtungen dieselbe Steifigkeit. Beispielsweise ist eine Stahlplatte eine isotrope Fläche. Orthotrope Flächen besitzen entlang der X und Y-Achsen des lokalen Koordinatensystems unterschiedliche Steifigkeiten. Ein Beispiel hierfür sind Brettschichtholzplatten.
Faltwerkselement besitzt orthotrope Eigenschaften
Nur wenn sie diese Schaltfläche aktivieren, können sie dem Faltwerkselement orthotrope Eigenschaften zuweisen.
Standardwerte übernehmen
Bei Betätigung dieser Befehlsschaltfläche werden die momentanen isotropen Eigenschaften des Faltwerkselementes auf den Dialog übernommen. So müssen nur die Werte eingegeben werden, die von den isotropen Eigenschaften abweichen.
Definitionsarten
Folgende Eingabemöglichkeiten stehen zur Verfügung:
- Unterschiedliche Dicken in den beiden Richtungen
- Unterschiedliche Elastizitäten in den beiden Richtungen
- Eine Kombination aus den beiden ersten Möglichkeiten
Abweichende Dicke in Y-Richtung
Für die Ermittlung der Steifigkeit in Y-Richtung kann eine abweichende Dicke eingegeben werden. Es handelt sich um die Y-Achse im lokalen Koordinatensystem des Faltwerkselements.
Diese Dicke wird lediglich zur Ermittlung der Steifigkeiten berücksichtigt. Die Bemessung und Ermittlung des Eigengewichts, der Spannungen sowie der Steifigkeit in X-Richtung erfolgt mit der Dicke, die auf dem Reiter "Standard" eingegeben ist.
Diese Dicke wird lediglich zur Ermittlung der Steifigkeiten berücksichtigt. Die Bemessung und Ermittlung des Eigengewichts, der Spannungen sowie der Steifigkeit in X-Richtung erfolgt mit der Dicke, die auf dem Reiter "Standard" eingegeben ist.
Elastizitäten für die Platte
Geben Sie hier die Materialkennwerte des isotropen Materials an.
Scheibenelastizität unterschiedlich von Plattenelastizität
Wenn Sie diese Schaltfläche aktivieren, können sie dem Faltwerkselement in der Scheibenrichtung andere Elastizitäten als in der Plattenrichtung zuweisen. Ein Anwendungsfall hierfür sind z.B. Brettschichthölzer.
| Ex, Platte | E-Modul in X-Richtung der Platte |
| Ey, Platte | E-Modul in Y-Richtung der Platte |
| Gxy, Platte | G-Modul in Z-Richtung der Platte |
| μxy, Platte | Querdehnzahl der Platte |
| Gxz | G-Modul in X-Richtung der Platte, Querschub |
| Gyz | G-Modul in Y-Richtung der Platte, Querschub |
| _ | _ |
| Ex, Scheibe | E-Modul in X-Richtung der Scheibe |
| Ey, Scheibe | E-Modul in Y-Richtung der Scheibe |
| Gxy, Scheibe | G-Modul in Z-Richtung der Scheibe |
| μxy, Scheibe | Querdehnzahl der Scheibe |
Aus den oben angegeben Werten erstellt das Programm die elastische Steifigkeitsmatrix.
Plattenanteil (Biegung)
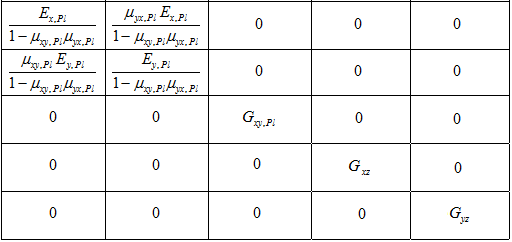
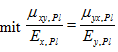
Scheibenanteil (Membrankräfte)

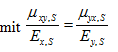
Jedes Faltwerkselement verfügt über ein Raster von Hilfslinien, um die graphische Eingabe von Aussparungen und Faltwerkselement-Einwirkungen zu erleichtern.
Die Richtung der Linien wird durch zwei Vektoren im lokalen Koordinatensystem angeben. Standardmäßig ist das Raster parallel zur lokalen X- bzw. Y-Achse. Der Nullpunkt legt fest, wo sich das erste Paar Hilfslinien schneidet. Standardmäßig ist das der Ursprung des lokalen Koordinatensystems. Der Abstand der Hilfslinien kann durch Rasterhöhe und -breite beeinflusst werden.
Wird ein Faltwerkselement mit Hilfe einer Arbeitsebene erzeugt, so werden alle das Raster betreffenden Einstellungen von dieser übernommen. Wird ein Faltwerkselement ohne Verwendung einer Arbeitsebene erzeugt, so ist das Raster standardmäßig identisch mit dem lokalen Koordinatensystem.
Die Richtung der Linien wird durch zwei Vektoren im lokalen Koordinatensystem angeben. Standardmäßig ist das Raster parallel zur lokalen X- bzw. Y-Achse. Der Nullpunkt legt fest, wo sich das erste Paar Hilfslinien schneidet. Standardmäßig ist das der Ursprung des lokalen Koordinatensystems. Der Abstand der Hilfslinien kann durch Rasterhöhe und -breite beeinflusst werden.
Wird ein Faltwerkselement mit Hilfe einer Arbeitsebene erzeugt, so werden alle das Raster betreffenden Einstellungen von dieser übernommen. Wird ein Faltwerkselement ohne Verwendung einer Arbeitsebene erzeugt, so ist das Raster standardmäßig identisch mit dem lokalen Koordinatensystem.
Nullpunkt
Eine Position, die den Nullpunkt des Rasters innerhalb des lokalen Koordinatensystems festlegt. In dieser Position treffen sich zwingend zwei Linien des Rasters.
X-Richtung
Der Vektor, welcher die X-Richtung des Rasters innerhalb des lokalen Koordinatensystems festlegt.
Y-Richtung
Der Vektor, welcher die Y-Richtung des Rasters innerhalb des lokalen Koordinatensystems festlegt.
Rasterhöhe
Die Höhe eines Feldes im Raster. [m]
Rasterbreite
Die Breite eines Feldes im Raster. [m]
